FAQ/ Calculation of river water level in the event of a jet flow¶
If a jet occurs, is the river level of the jet flow output?
If there is a river that contains a steep section of the river channel, especially a section of the river channel where the Fr number of Fr is greater than 1, a mixture of normal and projectile flow will occur. Can DioVISTA calculate for this flow?
And if so, what kind of method is used to calculate the flow of mixed normal flow? In the technical reference, the river channel model is calculated by the leepfrog windward difference, but is it possible to calculate the interval where the radiation develops in such a simple way in a stable manner? Do you have any special ingenuity?
response¶
DioVISTA's indefinite flow (time-varying flow) uses equations of motion and does not solve normal and projectile currents separately. In order to realize stable calculations, we have made some original efforts. We do not disclose the details of these methods, so we will refrain from answering the details.
DioVISTA's unequal flow (flow without changing time) uses the law of conservation of energy, which separates the current, projectile, and jumping water.
We have not verified which slope a river becomes unstable atweighed by, but there is a document that summarizes the reproducibility of normal flow mixing, so we will show some of them.
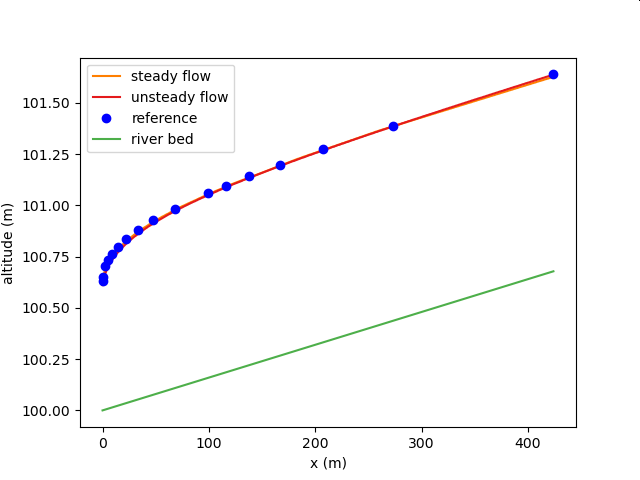
Comparison with One-Dimensional Heteroflow Analysis Part 1 (Normal Flow)¶
| Target waterways | Artificial waterways |
| Waterway conditions | A trapezoidal sectional prism channel with a bottom width b = 6 m, a slope of the shore z = 2, a slope S ~ 0 ~ = 0.0016, and a roughness factor of n = 0.025 flows a flow rate Q = 10 m ^3/s. The downstream end is a cliff. However, the energy coefficient alpha = 1.10. |
| Compare to | Yoshimi Okamoto Hydraulics Explanation of Open Waterways p. 180, Example 4.2 |
| Calculation conditions to be compared | One-dimensional unequal flow calculation using the law of conservation of energy (direct sequential method) |
Calculation result
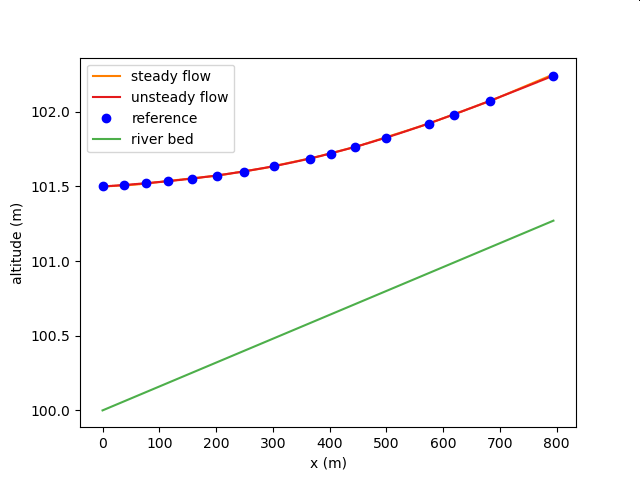
Comparison with One-Dimensional Unequal Flow Analysis Part 2 (Normal Flow)¶
| Target waterways | Artificial waterways |
| Waterway conditions | A trapezoidal sectional prism channel with a bottom width b = 6 m, a slope of the shore z = 2, a slope S ~ 0 ~ = 0.0016, and a roughness factor of n = 0.025 flows a flow rate Q = 10 m ^3/s. When a wide summit weir was built at the downstream end of this channel, the depth of the water directly upstream of the weir was 1.5 m. However, the energy coefficient alpha = 1.10. |
| Compare to | Yoshimi Okamoto Hydraulics Explanation of Open Waterways p. 188, Example 4.5 |
| Calculation conditions to be compared | One-dimensional unequal flow calculation using the law of conservation of energy (standard sequential method) |
Calculation result
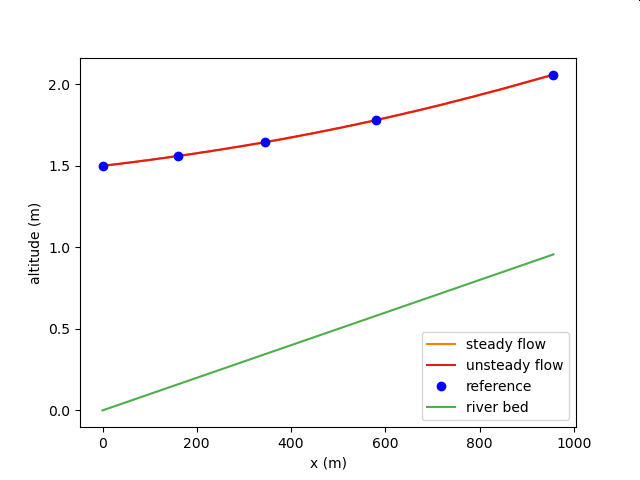
Comparison with One-Dimensional Imequal Flow Analysis Part 3 (Normal Flow)¶
| Target waterways | Artificial waterways |
| Waterway conditions | There is a concrete rectangular section channel with a width of 2 m and a bottom slope of 1/1000. A flow rate of 3.0 m^3/s flows through it, and a weir is provided at the downstream end of the channel. The depth of the water immediately before the weir shall be 1.5 m. The roughness coefficient of manning of the channel is n = 0.014 and the energy coefficient alpha = 1.0. |
| Compare to | Taizo Hayashi Basic Hydraulics p. 268, Example 1 |
| Calculation conditions to be compared | One-dimensional unequal flow calculation using the law of conservation of energy (direct sequential method) |
Calculation result
Comparison with One-Dimensional Heteroflow Analysis Part 4 (Normal Flow)¶
| Target waterways | Artificial waterways |
| Waterway conditions | A 70 m long reinforced concrete culvert with a square section of 1.6 m × 1.6 m in the internal method of steadily releasing 7 m^3/s of water from the reservoir. The slope of the culvert is 1/50, Manning's roughness coefficient is n=0.014, and the energy coefficient alpha=1.0. |
| Compare to | Taizo Hayashi Basic Hydraulics p. 271, Example 2 |
| Calculation conditions to be compared | One-dimensional unequal flow calculation using the law of conservation of energy (direct sequential method) |
Calculation result
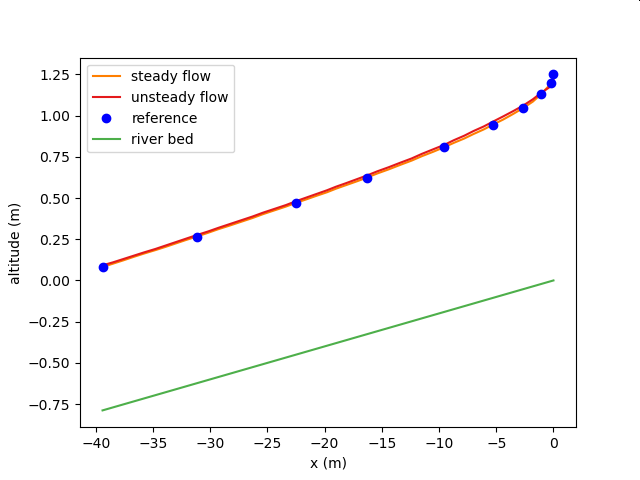
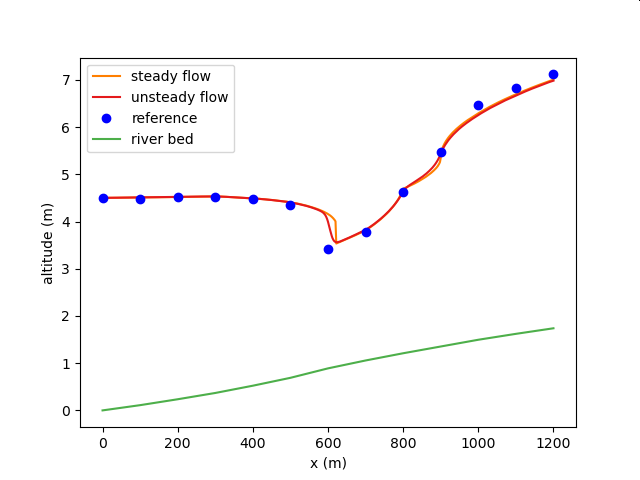
Comparison with One-Dimensional Unequal Flow Analysis Part 5 (Mixed Normal Flow)¶
| Target waterways | Artificial waterways |
| Waterway conditions | A trapezoidal sectional prism channel with a bottom width b = 6 m, a slope of the shore z = 2, a slope S ~ 0 ~ = 0.0016, and a roughness factor of n = 0.025 flows a flow rate Q = 10 m ^3/s. It bends from a certain point and the slope changes to S0=0.02. However, the energy coefficient alpha = 1.10. |
| Compare to | Yoshimi Okamoto Hydraulics Explanation of Open Waterways p. 184, Example 4.4 |
| Calculation conditions to be compared | One-dimensional unequal flow calculation using the law of conservation of energy (direct sequential method) |
Calculation result
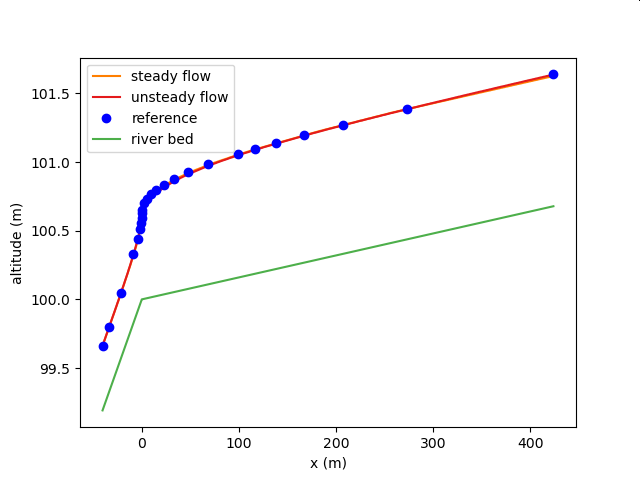
Comparison with One-Dimensional Unequal Flow Analysis Part 6 (Mixed Normal Flow)¶
| Target waterways | Artificial waterways |
| Waterway conditions | Water with a flow rate of Q = 1,000 m 3/s flows into a rectangular cross-section river with varying channel width. However, Manning's roughness coefficient n = 0.025, energy coefficient alpha = 1.1, downstream water level is 4.5 m, channel width b, riverbed gradient, and distance x of 12 sections from the downstream end are as shown in the table below. |
| Compare to | Taizo Hayashi Basic Hydraulics p. 277, Example |
| Calculation conditions to be compared | One-dimensional unequal flow calculation using the law of conservation of energy (standard sequential method) |

Calculation result